Exercise solution for Chapter 8, Part 1
Exercise 8.1
Do the analyses of Section 8.5 with the
edgeRpackage and compare the results: make a scatterplot of the log 10 p-values, pick some genes where there are large differences, and visualize the raw data to see what is going on. Based on this can you explain the differences?
Most of the following code is taken straight from the book in section 8.5 for data cleaning/wrangling and the DESeq2 analysis. The steps performed in edgeR are quite similar but we do see some differences that we will get to towards the end.
First, we load our libraries.
library(pasilla)
library(edgeR)
library(dplyr)
library(DESeq2)
library(ggplot2)
library(pheatmap)
library(tidyverse)We will use the same data used in the DESeq2 examples from the section 8.5.
Load the example data using the system.file() call for R data stored as part of a R package.
We then convert our data to a matrix object called counts.
fn = system.file("extdata", "pasilla_gene_counts.tsv",
package = "pasilla", mustWork = TRUE)
counts = as.matrix(read.csv(fn, sep = "\t", row.names = "gene_id"))
head(counts)## untreated1 untreated2 untreated3 untreated4 treated1 treated2
## FBgn0000003 0 0 0 0 0 0
## FBgn0000008 92 161 76 70 140 88
## FBgn0000014 5 1 0 0 4 0
## FBgn0000015 0 2 1 2 1 0
## FBgn0000017 4664 8714 3564 3150 6205 3072
## FBgn0000018 583 761 245 310 722 299
## treated3
## FBgn0000003 1
## FBgn0000008 70
## FBgn0000014 0
## FBgn0000015 0
## FBgn0000017 3334
## FBgn0000018 308The matrix tallies the number of reads seen for each gene in each sample. We call it the count table. It has 14599 rows, corresponding to the genes, and 7 columns, corresponding to the samples.
dim(counts)## [1] 14599 7edgeR
Now begins the analysis with the edgeR package. To do this, we follow the vignette for the package that is a downloadable .pdf file that you can get in your Rstudio session vignette("edgeR") or online with https://www.bioconductor.org/packages/release/bioc/vignettes/edgeR/inst/doc/edgeRUsersGuide.pdf.
Here we make the group object which is a vector with values representing the treatment status of each of the 7 samples, where 1 refers to the untreated group, and 2 refers to the treated group. With this group object we can make a DGEList(), from the edgeR package, with our count data and the groups we just made. A DGEList() object is very similar to any traditional R list object and can be manipulated like any other list in R.
group <- factor(c(1,1,1,1,2,2,2))
x <- DGEList(counts=counts, group=group)RNA-seq provides a measure of the relative abundance of each gene in each RNA
sample, but does not provide any measure of the total RNA output on a per-cell basis. In other words, RNA-seq measures relative expression rather than absolute expression. This can become an issue in RNA-seq when a small number of highly expressed genes consume a substantial proportion of the total library for a sample causing under sampling of the other expressed genes.
To help combat this we turn to normalization. calcNormFactors normalizes by finding a set of scaling factors for the library sizes that minimizes the log-fold changes between the samples for most genes. Using a trimmed mean of M-values (TMM) between each pair of samples. If we receive a norm.factors \(\lt\) 1 that means a small number of high count genes are monopolizing the sequencing reducing the counts of other genes. Conversely, a norm.factors \(\gt\) 1 scales up the library size, analogous to downscaling the counts. This normalization can help account for things like varying sequencing depth, length of genes, and RNA composition.
normalization <- calcNormFactors(x)
normalization## An object of class "DGEList"
## $counts
## untreated1 untreated2 untreated3 untreated4 treated1 treated2
## FBgn0000003 0 0 0 0 0 0
## FBgn0000008 92 161 76 70 140 88
## FBgn0000014 5 1 0 0 4 0
## FBgn0000015 0 2 1 2 1 0
## FBgn0000017 4664 8714 3564 3150 6205 3072
## treated3
## FBgn0000003 1
## FBgn0000008 70
## FBgn0000014 0
## FBgn0000015 0
## FBgn0000017 3334
## 14594 more rows ...
##
## $samples
## group lib.size norm.factors
## untreated1 1 13972512 0.9995731
## untreated2 1 21911438 1.0081519
## untreated3 1 8358426 0.9843974
## untreated4 1 9841335 0.9525077
## treated1 2 18670279 1.0651817
## treated2 2 9571826 0.9957012
## treated3 2 10343856 0.9978557The model.matrix() function creates a design matrix which is a matrix of values of explanatory variables of a set of objects. Each row represents an individual object, with the successive columns corresponding to the variables and their specific values for that object. The purpose of this conversion is to prepare the data in a manner that facilitates regression-like modelling (ex. glm).
design <- model.matrix(~group)
head(design)## (Intercept) group2
## 1 1 0
## 2 1 0
## 3 1 0
## 4 1 0
## 5 1 1
## 6 1 1The estimateDisp() function, “Maximizes the negative binomial likelihood to give the estimate of the common, trended and tagwise dispersions across all tags.” We have to use this negative binomial (aka gamma-Poisson) model since our experiments vary from replicate to replicate more than the traditional Poisson can account for. This variance can be due to seemingly miniscule experimental conditions such as, temperature of cell culture, pipettor calibration, etc. In the case of the gamma-Poisson we have two inputs for variance and mean instead of just having \(\lambda\) for both variance and mean in the normal Poisson.
An important consideration that the edgeR package has taken into account is the fact that RNA-seq and other Next Generation Sequencing projects are extremely expensive and generally have few samples. Accounting for dispersion with a small number of samples can be challenging and the edgeR package tackles this conundrum using a qCML method. The qCML method calculates the likelihood by conditioning on the total counts for each tag, and uses pseudo counts after adjusting for library sizes. Given a table of counts or a DGEList object, the qCML common dispersion and tagwise dispersions can be estimated using the estimateDisp() function.
design_matrix <- estimateDisp(normalization, design)
design_matrix## An object of class "DGEList"
## $counts
## untreated1 untreated2 untreated3 untreated4 treated1 treated2
## FBgn0000003 0 0 0 0 0 0
## FBgn0000008 92 161 76 70 140 88
## FBgn0000014 5 1 0 0 4 0
## FBgn0000015 0 2 1 2 1 0
## FBgn0000017 4664 8714 3564 3150 6205 3072
## treated3
## FBgn0000003 1
## FBgn0000008 70
## FBgn0000014 0
## FBgn0000015 0
## FBgn0000017 3334
## 14594 more rows ...
##
## $samples
## group lib.size norm.factors
## untreated1 1 13972512 0.9995731
## untreated2 1 21911438 1.0081519
## untreated3 1 8358426 0.9843974
## untreated4 1 9841335 0.9525077
## treated1 2 18670279 1.0651817
## treated2 2 9571826 0.9957012
## treated3 2 10343856 0.9978557
##
## $design
## (Intercept) group2
## 1 1 0
## 2 1 0
## 3 1 0
## 4 1 0
## 5 1 1
## 6 1 1
## 7 1 1
## attr(,"assign")
## [1] 0 1
## attr(,"contrasts")
## attr(,"contrasts")$group
## [1] "contr.treatment"
##
##
## $common.dispersion
## [1] 0.0228685
##
## $trended.dispersion
## [1] 0.12060195 0.04196786 0.11986264 0.12040360 0.01632837
## 14594 more elements ...
##
## $tagwise.dispersion
## [1] 0.12060195 0.02742256 0.70902130 0.09430132 0.01321566
## 14594 more elements ...
##
## $AveLogCPM
## [1] -2.636763 2.953356 -1.966526 -2.223010 8.454625
## 14594 more elements ...
##
## $trend.method
## [1] "locfit"
##
## $prior.df
## [1] 5.886884
##
## $prior.n
## [1] 1.177377
##
## $span
## [1] 0.3013916Now that we have our design_matrix we can begin fitting modified linear models to it. Here we use a quasi-likelihood negative binomial generalized log-linear model, which is a mouth full. “Quasi-likelihood estimation is one way of allowing for overdispersion, that is, greater variability in the data than would be expected from the statistical model used.” Since we have already stated that we will have variation in our experiments, possibly due to the most minute factors, this issue of overdispersion is apparent. Instead of using traditional probability functions, a variance function is used (variance as a function of the mean) and allows for an overdispersion parameter input which is used to “fix” the variance function to resemble that of an existing probability function (ex. Poisson).
The goal of this fit is to identify genes where the intensity level (gene expression level) is notably different between our treated and untreated groups.
Running the glmQLF...() functions gives the null model against which the full model is compared. Tags can then be ranked in order of evidence for differential expression, based on the p-value computed for each tag.
fit <- glmQLFit(design_matrix, design)
qlf <- glmQLFTest(fit, coef=2)
edgeRoutput <- topTags(qlf)
edgeRoutput## Coefficient: group2
## logFC logCPM F PValue FDR
## FBgn0039155 -4.601317 5.882317 953.1722 1.646470e-14 2.403682e-10
## FBgn0025111 2.905756 6.923428 714.2877 1.257310e-13 9.177735e-10
## FBgn0035085 -2.548257 5.684922 452.3866 3.068717e-12 1.311741e-08
## FBgn0003360 -3.173036 8.452776 442.2207 3.594058e-12 1.311741e-08
## FBgn0029167 -2.188103 8.221274 412.0926 5.866109e-12 1.404698e-08
## FBgn0039827 -4.142255 4.397963 408.8548 6.195926e-12 1.404698e-08
## FBgn0034736 -3.492036 4.186934 403.9614 6.735313e-12 1.404698e-08
## FBgn0029896 -2.434452 5.305827 336.3777 2.386477e-11 4.355023e-08
## FBgn0000071 2.685868 4.795202 288.1793 6.900283e-11 1.119303e-07
## FBgn0034434 -3.624878 3.214994 282.6144 7.884818e-11 1.151105e-07head(as.data.frame(qlf))## logFC logCPM F PValue
## FBgn0000003 1.90105753 -2.636763 1.40991069 0.25938432
## FBgn0000008 0.01020453 2.953356 0.00282599 0.95833875
## FBgn0000014 -0.21077864 -1.966526 0.03020978 0.86444776
## FBgn0000015 -1.61118380 -2.223010 1.65428857 0.21877991
## FBgn0000017 -0.23044399 8.454625 3.99686462 0.06492692
## FBgn0000018 -0.09673451 5.088412 0.53070377 0.47805393Our outputs can be summarized by looking at our logFC column (log fold change) where the higher the number the higher the count of that particular gene was read during the sequencing run. Secondly our PValue, if it meets threshold (typically pvalue <= 0.05) allows the rejection of our null hypothesis, which is, there is equal expression regardless of what gene you look at.
Now we want to visualize the data points after their regression fits. We must tidy up the data sets a bit to apply some tidyverse magic. First the data is converted to a data frame, using as.data.frame(), then we use the rownames_to_column() function which sounds like its name, and pulls the row names, in this case gene_id, into a new column of the dataframe. Lastly, we subset the data using the select() function for only the columns we want, and order the data using the arrange() function to start with the largest values with respect to the padj via the desc() argument inside arrange().
tidy_pasilla <- pasilla %>%
results() %>%
as.data.frame() %>%
rownames_to_column(var = "gene_id") %>%
select(gene_id, pvalue, padj) %>%
arrange(desc(padj))
tidy_edgeR <- qlf %>%
as.data.frame() %>%
rownames_to_column(var = "gene_id") %>%
select(gene_id, PValue)Using full_join() from dplyr package we are able to subset these two data frames based on the gene_id column and keeping all other matching columns.
full_join(tidy_pasilla, tidy_edgeR,
"gene_id") %>%
ggplot(aes(x = pvalue, y = PValue)) +
labs(x = "DESeq2 pvalue", y = "edgeR PValue") +
scale_x_log10() +
scale_y_log10() +
geom_point(alpha = 0.5) +
geom_abline(slope = 1, intercept = 0, color = "blue") +
geom_vline(xintercept = 1e-25, color = "red") +
ggtitle("DESeq2 vs EdgeR", subtitle = "Each point represents a single gene, p-value is for whether
the gene has differential expression between groups") +
theme_bw()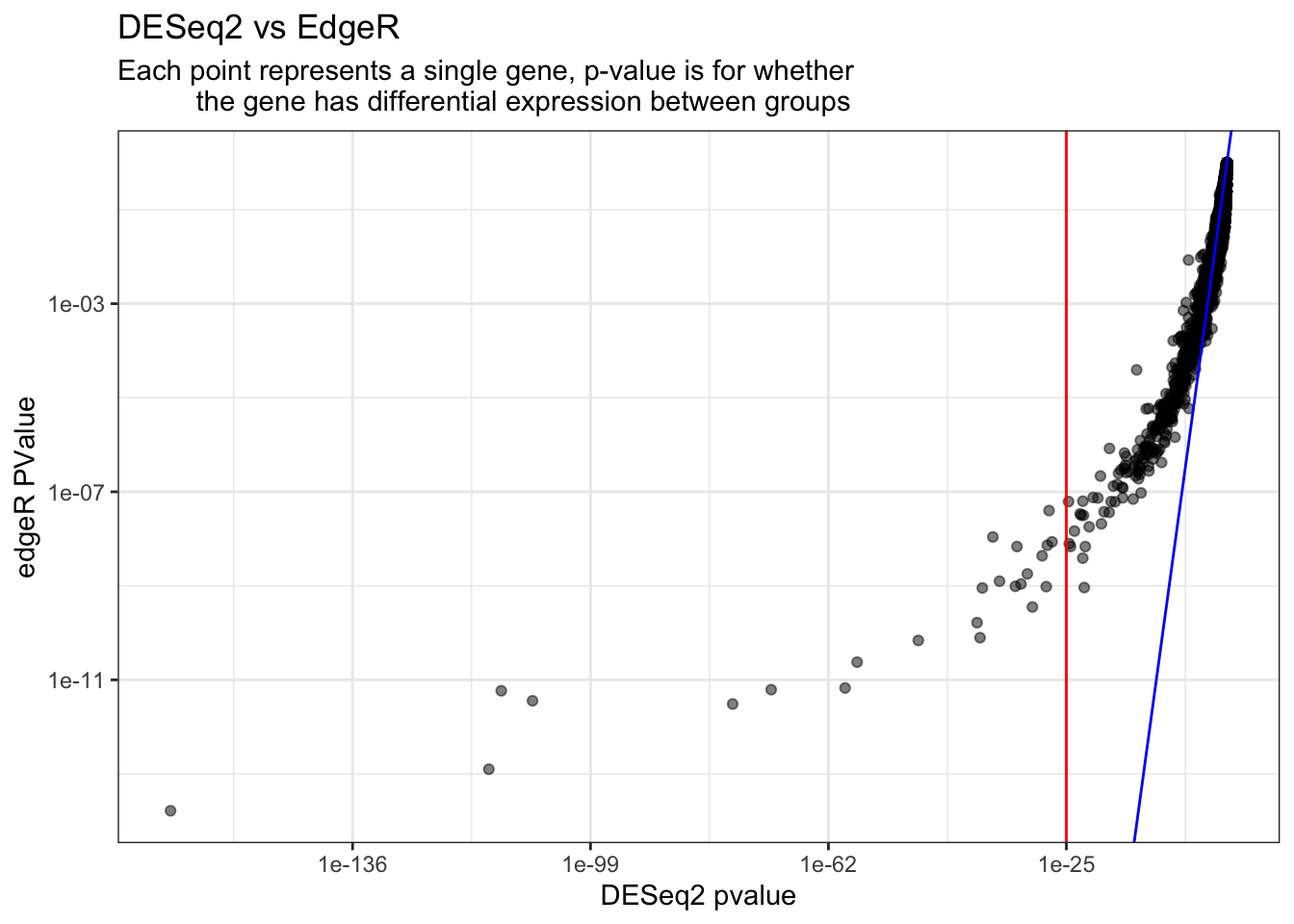
The reference line drawn in blue here using geom_abline() is to show what the data would look like if the two methods were identical.
Looking at the graph above, we see that most of the data are falling relatively close to one another when our pvalue \(\gt\) 1e-25. We know this because the alpha of the ggplot object is set to 0.5, so if we see a black dot, it means there are two points, one on top of each other. This is what we would expect considering these packages DESeq2 and edgeR have the same purpose in mind and is why we are comparing their outputs in this exercise!
Below we subset the data again, this time selecting those points with pvalues \(\leq\) 1e-25 (log10 transform). When plotting these we don’t see much overlapping, supporting the variation between the edgeR and DESeq2 modes of analysis.
full_join(tidy_pasilla, tidy_edgeR,"gene_id") %>%
filter(pvalue <= 1e-25) %>%
ggplot(aes(x = pvalue, y = PValue)) +
labs(x = "DESeq2 pvalue", y = "edgeR PValue") +
geom_point(alpha = 0.5) +
scale_x_log10() +
scale_y_log10() +
ggtitle("Genes with DESeq pvalue <= -25", subtitle = "Each point represents a single gene, p-value is for whether
the gene has differential expression between groups") +
theme_bw()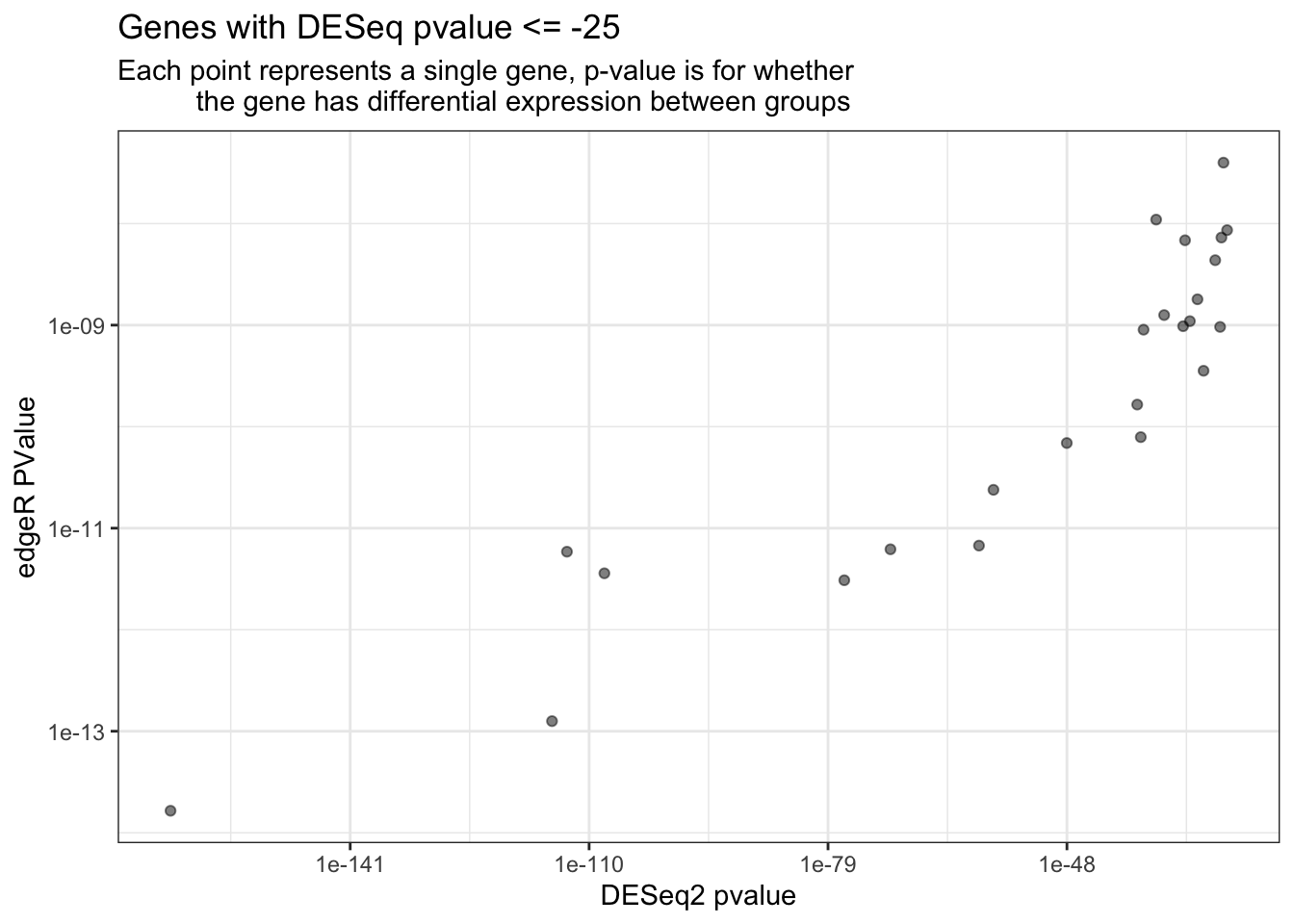
References
- https://www.bioconductor.org/packages/release/bioc/vignettes/edgeR/inst/doc/edgeRUsersGuide.pdf
- https://en.wikipedia.org/wiki/Quasi-likelihood
- http://web.stanford.edu/class/bios221/book/Chap-CountData.html
- https://rstudio.com/wp-content/uploads/2015/02/rmarkdown-cheatsheet.pdf
- https://geanders.github.io/RProgrammingForResearch/